(Leetcode) 300 - Longest Increasing Subsequence 풀이
New Year Gift - Curated List of Top 75 LeetCode Questions to Save Your Time
위 링크에 있는 추천 문제들을 시간이 있을때마다 풀어보려고 한다.
https://leetcode.com/problems/longest-increasing-subsequence/description/
이 문제는 DP 문제이다.
해결 코드
class Solution:
def lengthOfLIS(self, nums: List[int]) -> int:
longest = 1
dp = [1] + ([float('-inf')] * (len(nums) - 1))
for i, num in enumerate(nums):
if i == 0:
continue
for j in range(0, i + 1):
if num > nums[j]:
dp[i] = max(dp[i], dp[j] + 1)
if dp[i] == float('-inf'):
dp[i] = 1
longest = max(longest, dp[i])
return longest
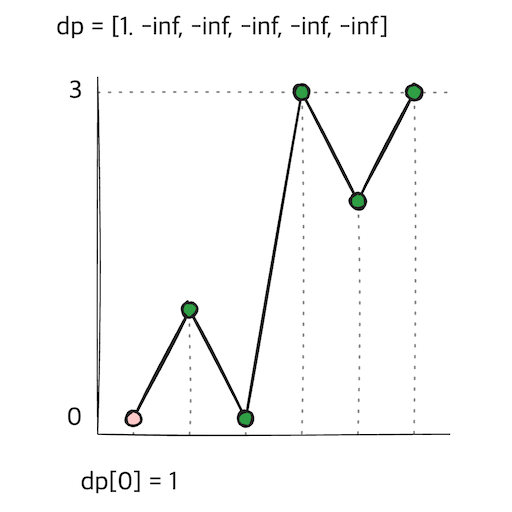
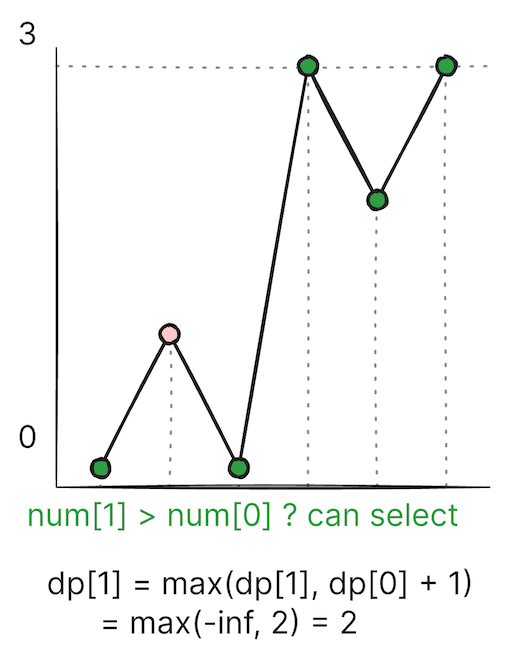
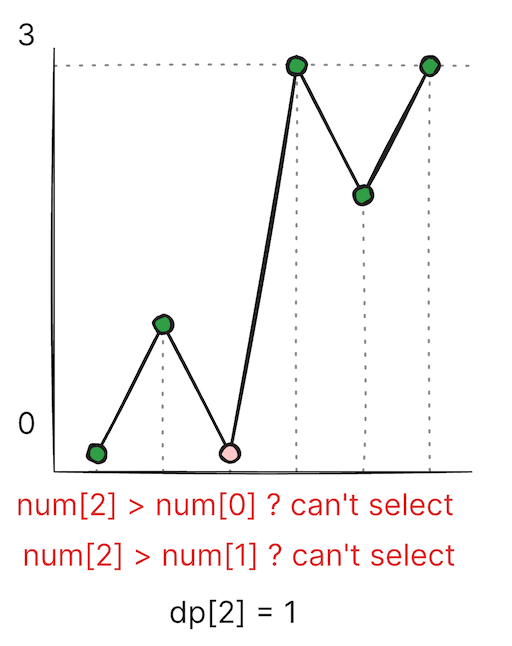
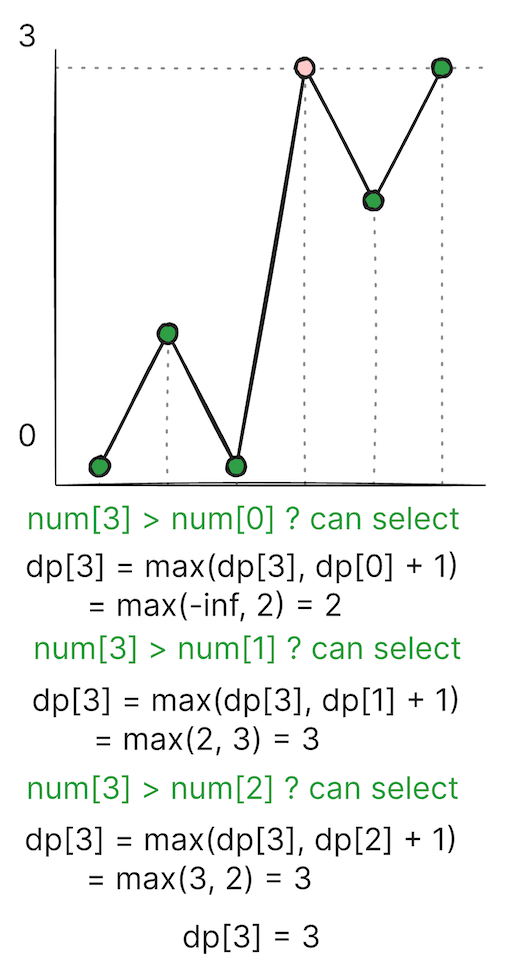
풀이
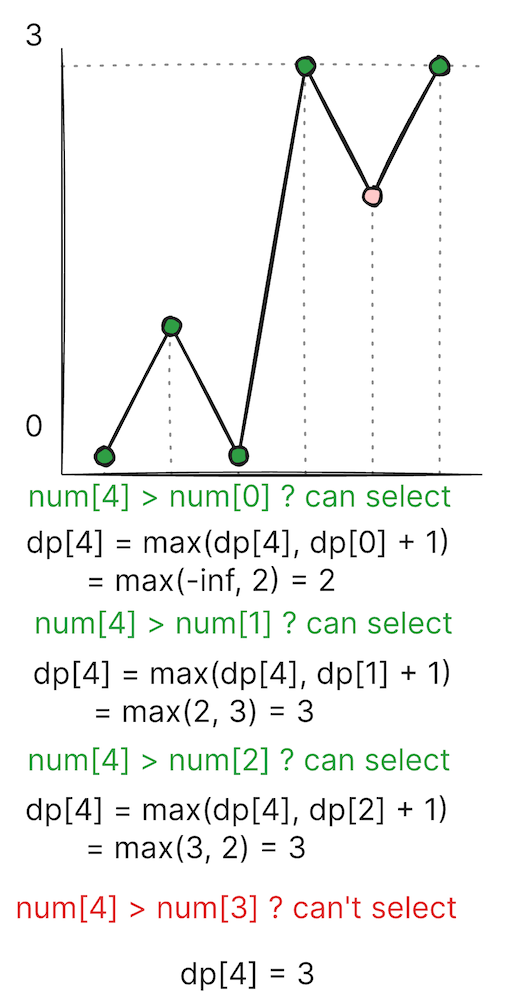
이 문제는 이전 값을 활용할 수 있는 문제이다.

다른 사람의 코드
이 코드는 간결하고, 속도도 빠르게 나온다.
class Solution:
def lengthOfLIS(self, nums: List[int]) -> int:
lst = []
for num in nums:
i = bisect_left(lst, num)
if i == len(lst):
lst.append(num)
else:
lst[i] = num
return len(lst)
bisect_left 이 뭐하는 애인가 싶어서 찾아보니 다음과 같았다.

bisect 는 배열 이진 분할 알고리즘 구현체이고 bisect_left는 정렬된 순서를 유지하도록 a에 x를 삽입할 위치를 찾아준다고 한다.
print(Solution().lengthOfLIS([0,1,0,3,2,3]))
num: 0
i: 0
append 0
lst [0]
num: 1
i: 1
append 1
lst [0, 1]
num: 0
i: 0
lst[i] = 0
lst [0, 1]
num: 3
i: 2
append 3
lst [0, 1, 3]
num: 2
i: 2
lst[i] = 2
lst [0, 1, 2]
num: 3
i: 3
append 3
lst [0, 1, 2, 3]
4 # 최종결과
Java 로 다시 풀기 (24.07.17)
Beats 62.23%
class Solution {
public int lengthOfLIS(int[] nums) {
int[] dp = new int[nums.length];
Arrays.fill(dp, 1);
int max = 1;
for (int i = 1; i < nums.length; i++) {
for (int j = 0; j < i; j++) {
if (nums[j] < nums[i]) {
dp[i] = Math.max(dp[j] + 1, dp[i]);
}
}
max = Math.max(max, dp[i]);
}
return max;
}
}
TC, SC
시간복잡도는 O(n^2), 공간복잡도는 O(n)이다.
Follow up 문제
Follow up: Can you come up with an algorithm that runs in O(n log(n)) time complexity?
파이썬 에서는 bisect_left 를 쓰면 된다고 하지만 자바에는 존재하지 않는다. 하지만 방법을 찾아보자.
dp 를 사용하지 않은 풀이 (Beats 82.20%)
우선은 ArrayList를 이용하여 비슷하게 모방해보았다.
public int lengthOfLIS(int[] nums) {
ArrayList<Integer> subsequence = new ArrayList<>();
subsequence.add(nums[0]);
for (int i = 1; i < nums.length; i++) {
int current = nums[i];
if(current > subsequence.get(subsequence.size() - 1)) {
subsequence.addLast(current);
} else if (current < subsequence.get(0)) {
subsequence.set(0, current);
} else {
for (int j = 1; j < subsequence.size(); j++) {
if(current > subsequence.get(j - 1) && current < subsequence.get(j)) {
subsequence.set(j, current);
}
}
}
}
return subsequence.size();
}
TC, SC
아직은 여전히 시간복잡도는 O(n^2), 공간복잡도는 O(n)이다. 빅오 표기법 상으로는 동일하나 실제 동작 시간은 감소하였다.
진짜 binary search를 도입해보기 (Beats 92.57%)
자바 Collections 에서는 binarySearch 메소드를 제공해준다. 적용해보면 다음과 같다.
public int lengthOfLIS(int[] nums) {
ArrayList<Integer> subsequence = new ArrayList<>();
for (int current : nums) {
// Collections.binarySearch : 목록에 포함된 경우 검색 키의 인덱스, 그렇지 않으면 (-(삽입점) - 1) 을 반환함.
int pos = Collections.binarySearch(subsequence, current);
if (pos < 0) pos = -(pos + 1);
if (pos >= subsequence.size()) {
subsequence.add(current);
} else {
subsequence.set(pos, current);
}
}
return subsequence.size();
}
Collections.binarySearch
해당 메소드의 리턴값은 다음과 같다.
목록에 포함된 경우 검색 키의 인덱스, 그렇지 않으면 (-(삽입점) - 1). 삽입 지점은 키가 목록에 삽입되는 지점, 즉 키보다 큰 첫 번째 요소의 인덱스 또는 목록의 모든 요소가 지정된 키보다 작은 경우 list.size()로 정의됩니다. 키가 발견되는 경우에만 반환값이 >= 0이 되도록 보장합니다.
TC, SC
시간복잡도는 O(n * logn), 공간복잡도는 O(n)이다.