(Leetcode) 207 - Course Schedule
New Year Gift - Curated List of Top 75 LeetCode Questions to Save Your Time
위 링크에 있는 추천 문제들을 시간이 있을때마다 풀어보려고 한다.
https://leetcode.com/problems/course-schedule/
그래프 문제. 위상 정렬으로 푸는 문제이다.
푸는데 너무 많은 시간이 소요되서 솔루션을 확인했고 습득해보는 방식으로 기록을 남겨본다.
사실 위상 정렬에 대한 부분을 모르고 있었다. 위상 정렬은 크게 dfs를 사용하는 방법과 kahn 알고리즘을 사용하는 방법이 있는데 이 문제에서는 kahn 알고리즘을 통해 해결하는 방식을 정리해본다.
이 문제를 읽다보면 prerequisite(선수 과목) 에 대한 이야기가 나오는데 위상정렬 위키페이지 를 들어가보면 딱 이 내용이 사례로 나온다. 문제가 위상 정렬에 대해서 아는지에 대한 질문이였던 것이다.
DFS로도 가능은 하지만 DFS의 경우 갯수가 많은경우 시간이 오래걸려서 힘들었고 그래서인지 대부분의 솔루션에서 Kahn 알고리즘으로 기반으로 설명하고 있었다. (DFS 솔루션도 있긴 했다.)
코드
class Solution:
def canFinish(self, n: int, prerequisites: List[List[int]]) -> bool:
adj = [[] for _ in range(n)]
indegree = [0] * n
ans = []
for pair in prerequisites:
course = pair[0]
prerequisite = pair[1]
adj[prerequisite].append(course)
indegree[course] += 1
queue = deque()
for i in range(n):
if indegree[i] == 0:
queue.append(i)
while queue:
current = queue.popleft()
ans.append(current)
for next_course in adj[current]:
indegree[next_course] -= 1
if indegree[next_course] == 0:
queue.append(next_course)
return len(ans) == n
설명
준비
Kahn 알고리즘 은 queue 를 사용한다.
예시로 다음과 같은 prerequisite가 주어졌다고 가정해보자.
[[0,1],[1,2],[0,3],[3,0]]
우선 그래프를 형성하면서 진입차수(indegree) 를 관리해야 한다. 진입차수는 해당 꼭지점(노드)로 향하는 edge의 수이다. (the number of head ends adjacent to a vertex - wiki)
데이터는 다음과 같이 구성된다.
# adj
[[3], [0], [1], [0]]
# indegree
[2, 1, 0, 1]
이미지화 하면 다음과 같다.
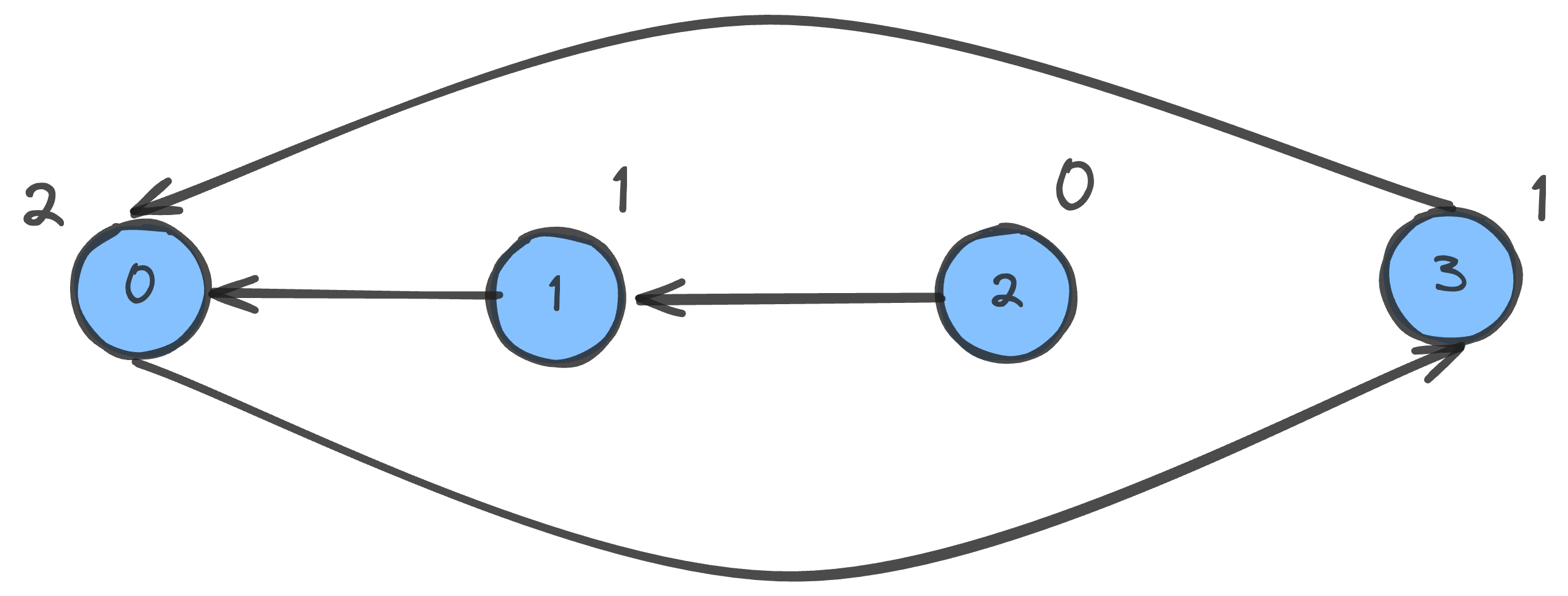
adj = [[] for _ in range(n)] indegree = [0] * n
queue를 로직 시작하기
먼저 차수가 0인 항목들을 queue에 담는다. 여기서는 index가 2인 node 가 해당된다. 다 넣었다면 다음 단계로 이동한다.
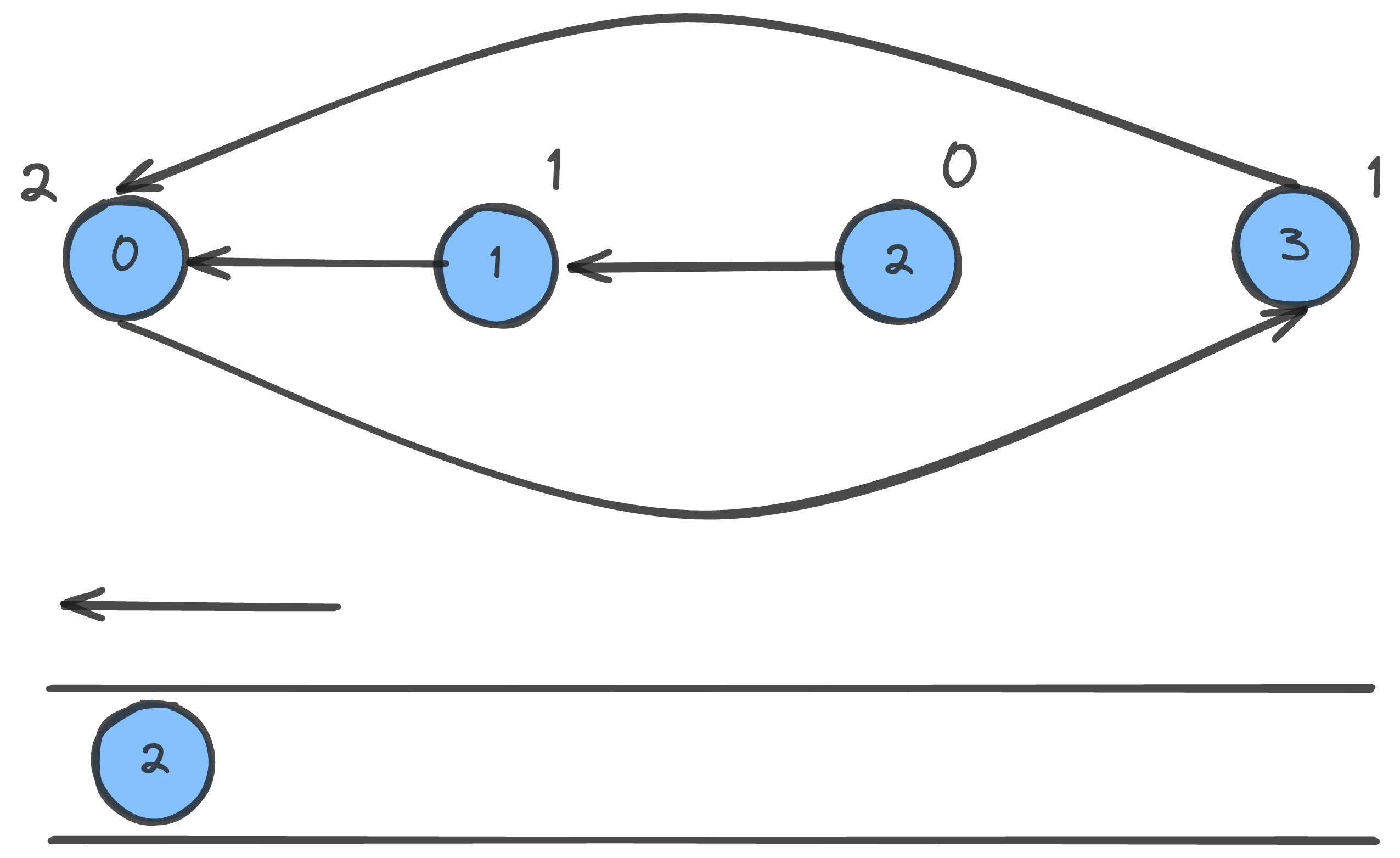
반복 수행
- queue에서 pop을 한다.
- ans에 index를 append한다.
- 해당 node에서 연결되는 다음 node에 대해서
- 진입차수에 -1을 한다.
- -1을 한 진입차수가 0이라면 큐에다 넣는다.
- queue가 비었다면 종료 아니라면 반복한다.
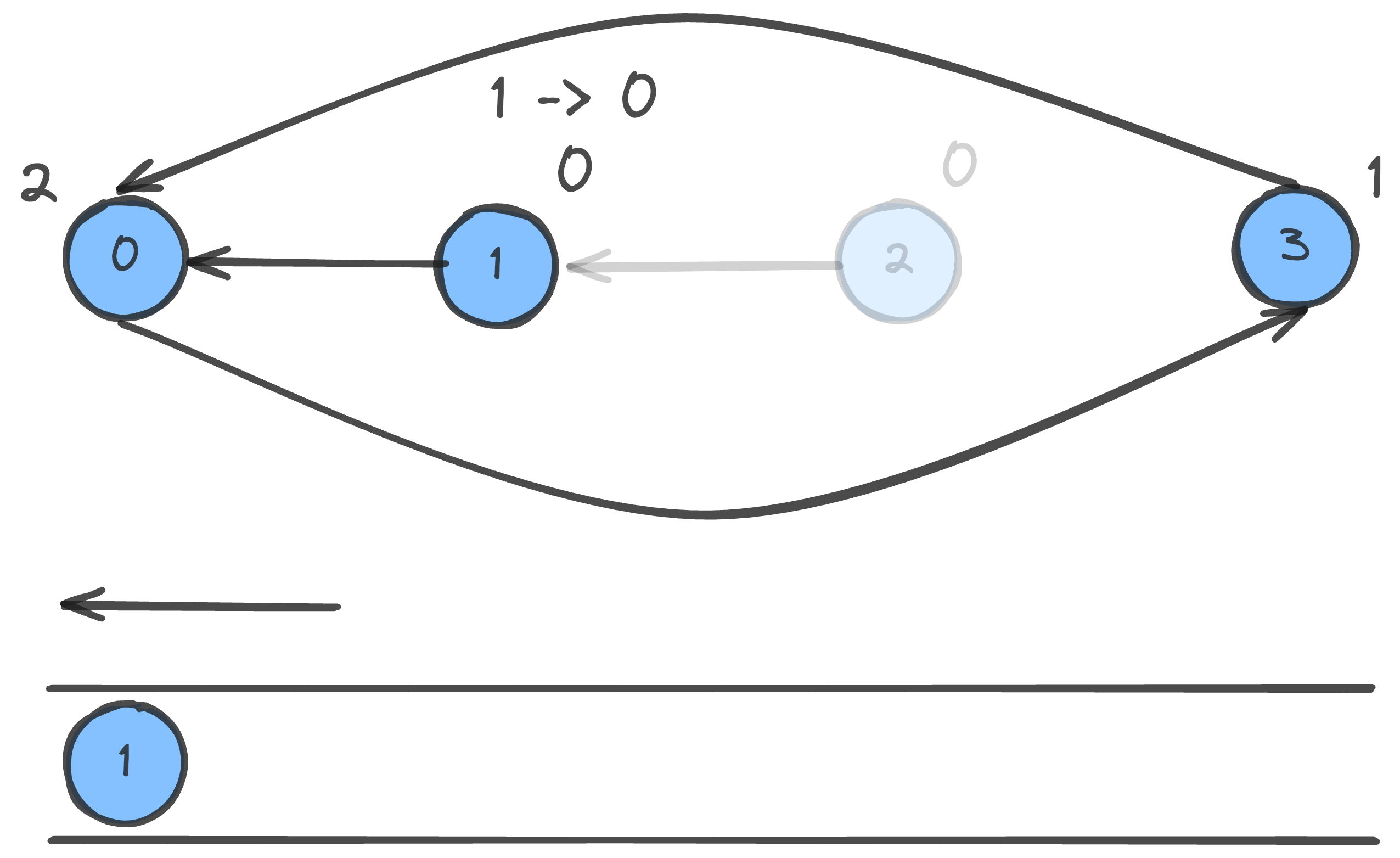
# 위 이미지에서
ans = [2]
이렇게 반복을 하면 내부에 순환이 있을 경우 다음과 같은 모양이 나오게 된다.
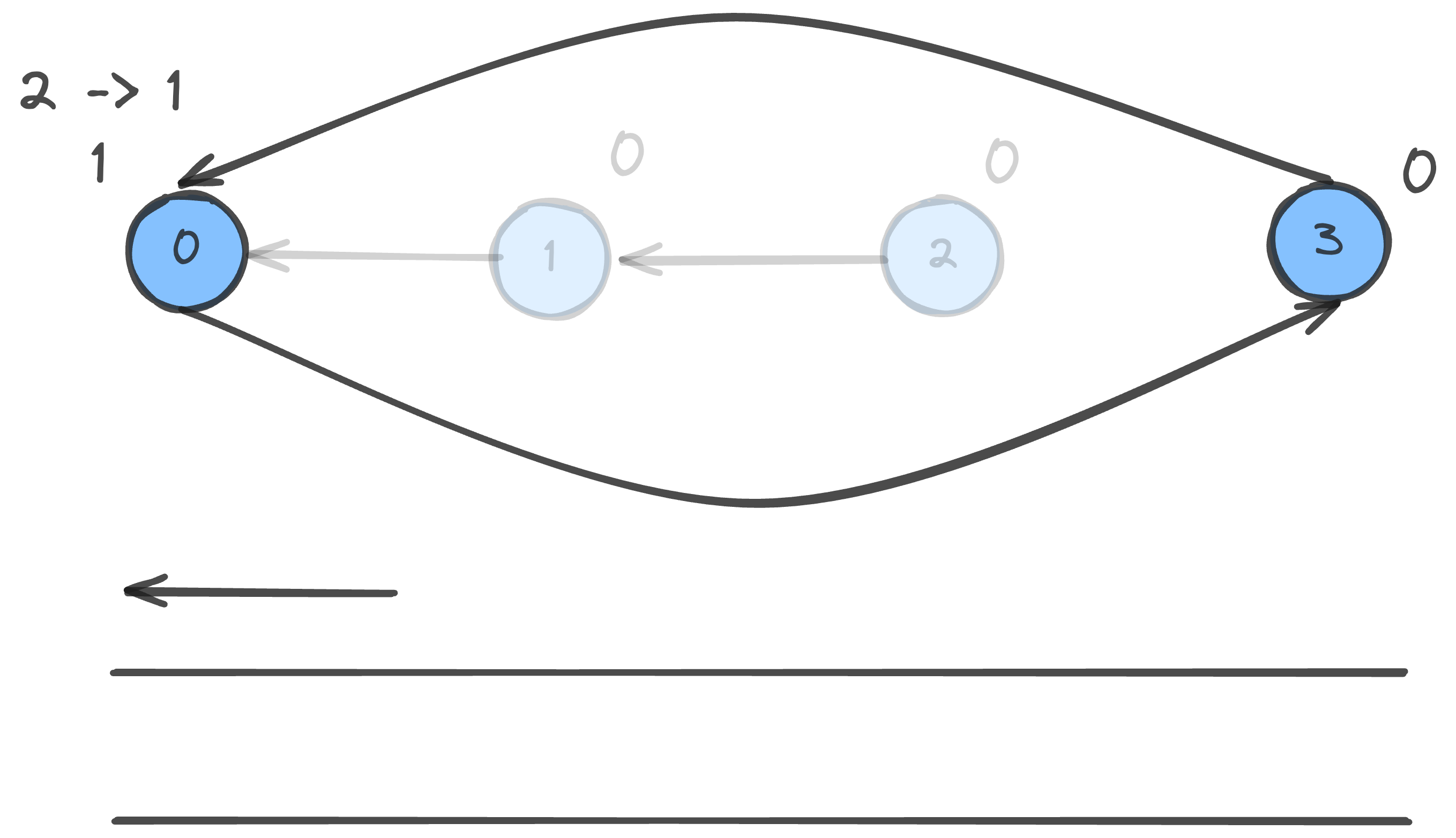
0 이 아니므로 queue에 넣지 않는다.
이 예시에서는 그러면 queue가 빈 상태가 되므로 반복 수행을 종료한다.
최종 결과
ans는 다음과 같은 값을 가진다.
ans = [2, 1]
따라서 아래의 return 문이 false를 반환하게 된다. (len(ans)는 2, n은 4 이다.)
return len(ans) == n
false를 반환했다는 것은 이건 주어진 prerequisite(선수 과목)에 오류(순환)가 있다는 뜻이다.
java로 다시 풀기 (24.06.30)
public class Solution {
public boolean canFinish(int numCourses, int[][] prerequisites) {
if (prerequisites.length == 0) {
return true;
}
Map<Integer, Node> vertexMap = new HashMap<>();
for (int[] prerequisite : prerequisites) {
vertexMap.putIfAbsent(prerequisite[0], new Node(prerequisite[0]));
vertexMap.putIfAbsent(prerequisite[1], new Node(prerequisite[1]));
Node vertex1 = vertexMap.get(prerequisite[0]);
Node vertex2 = vertexMap.get(prerequisite[1]);
vertex1.edges.add(vertex2);
vertex2.reversedEdges.add(vertex1);
}
Deque<Integer> deque = new LinkedList<>();
int[] degrees = new int[numCourses];
for (int i = 0; i < degrees.length; i++) {
Node vertex = vertexMap.get(i);
if (vertex != null) {
degrees[i] = vertex.edges.size();
if (degrees[i] == 0) {
deque.addLast(i);
}
}
}
while(!deque.isEmpty()) {
int vertexId = deque.removeFirst();
Node vertex = vertexMap.get(vertexId);
for (Node node : vertex.reversedEdges) {
degrees[node.id]--;
if (degrees[node.id] == 0) {
deque.addLast(node.id);
}
}
vertexMap.remove(vertexId);
}
return vertexMap.isEmpty();
}
}
class Node {
int id;
List<Node> edges;
List<Node> reversedEdges;
public Node(int id) {
this.id = id;
edges = new ArrayList<>();
reversedEdges = new ArrayList<>();
}
}
TC, SC
node(vertex)의 수를 V, edge의 수를 E 라고 하였을 때 시간 복잡도는 O(V + E) 이다. 공간 복잡도는 O(V + E)이다.