(Leetcode) 417 - Pacific Atlantic Water Flow
New Year Gift - Curated List of Top 75 LeetCode Questions to Save Your Time
위 링크에 있는 추천 문제들을 시간이 있을때마다 풀어보려고 한다.
https://leetcode.com/problems/pacific-atlantic-water-flow/description/
그래프 문제다. (정확하게는 matrix에서 dfs를 쓰는 문제다.)
푸는데 너무 많은 시간이 소요되서 솔루션 코드를 보고 이해하는 방식으로 기록을 남겨본다.
코드
class Solution:
def pacificAtlantic(self, heights: List[List[int]]) -> List[List[int]]:
rows, cols = len(heights), len(heights[0])
pac, atl = set(), set()
# Define DFS function to traverse the matrix and mark cells reachable
def dfs(r, c, visit, prevHeight):
# Base cases for termination of DFS traversal
if (
(r, c) in visit
or r < 0
or c < 0
or r == rows
or c == cols
or heights[r][c] < prevHeight
):
return
visit.add((r, c))
# Recursive calls for DFS traversal in four directions
dfs(r + 1, c, visit, heights[r][c])
dfs(r - 1, c, visit, heights[r][c])
dfs(r, c + 1, visit, heights[r][c])
dfs(r, c - 1, visit, heights[r][c])
# DFS from top and bottom borders to mark cells reachable by Pacific and Atlantic
for c in range(cols):
dfs(0, c, pac, heights[0][c])
dfs(rows - 1, c, atl, heights[rows - 1][c])
# DFS from left and right borders to mark cells reachable by Pacific and Atlantic
for r in range(rows):
dfs(r, 0, pac, heights[r][0])
dfs(r, cols - 1, atl, heights[r][cols - 1])
# Find cells reachable from both oceans and store their coordinates in res
res = []
for r in range(rows):
for c in range(cols):
if (r, c) in pac and (r, c) in atl:
res.append([r, c])
return res
설명
- 가장 자리에 있는 cell 부터 탐색을 시작한다.
- pac, atl 셋을 만들어 도달 가능 여부를 기록해둔다.
- 해당 cell이 pacific ocean 에 도달할 수 있다면 pac set에 추가하고
- 해당 cell이 atlantic ocean 에 도달할 수 있다면 atl set에 추가한다.
- 먼저 세로축을 탐색하고
- 이후에 가로축을 탐색한다.
- 각 셀의 상하좌우로 탐색 범위를 넓혀나간다.
- pac, atl 셋을 만들어 도달 가능 여부를 기록해둔다.
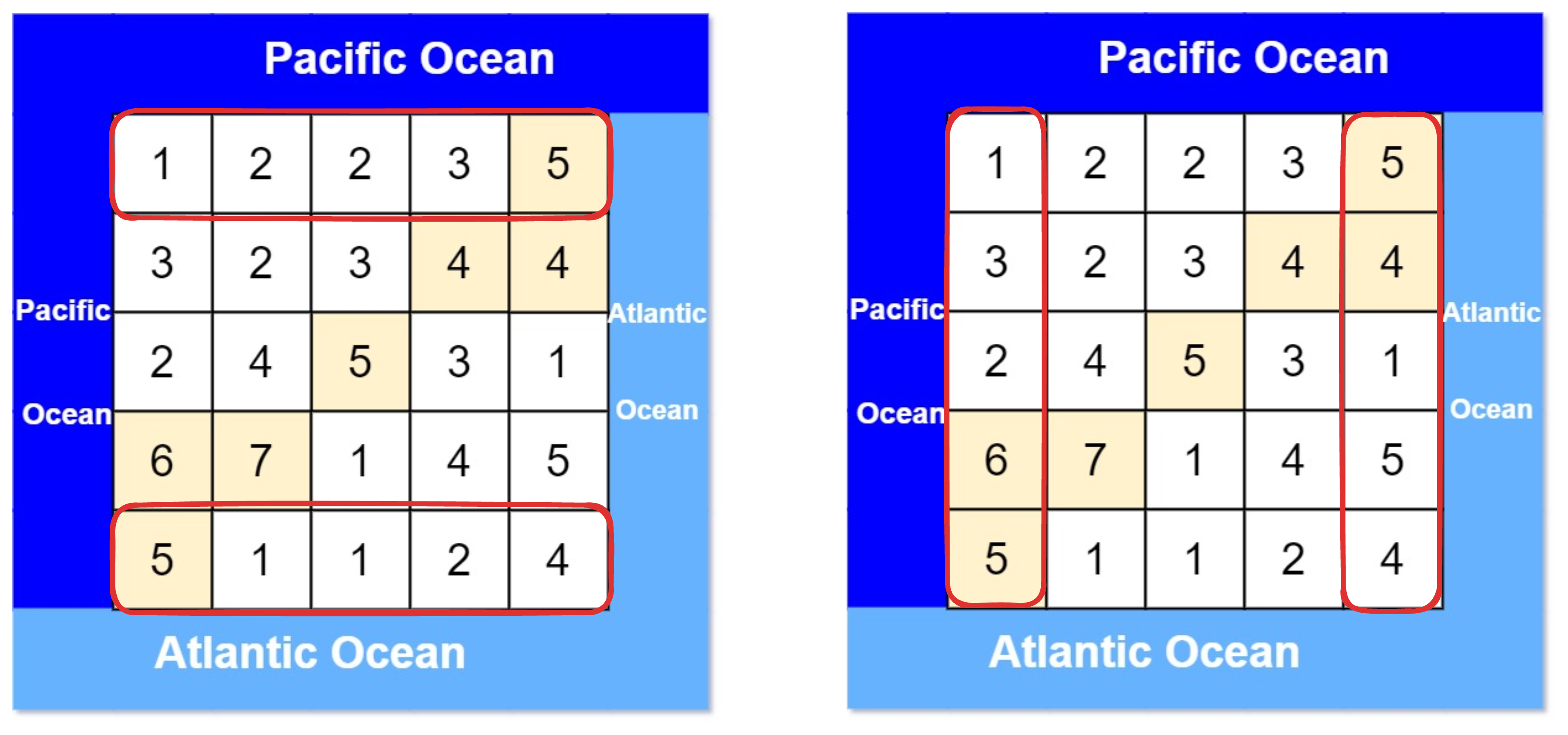
먼저 for c in range(cols): 에서 dfs(0, c, pac, heights[0][c]) 를 수행하므로 0,0 부터 탐색한다.
if (
(r, c) in visit
or r < 0
or c < 0
or r == rows
or c == cols
or heights[r][c] < prevHeight
):
조건에 걸리는 것이 없으므로
visit.add((r, c))
visit에 추가한다. (참고로 여기서 visit은 pac 이다.)
그 다음으로는 상하좌우의 셀들을 탐색하면 된다.
dfs(r + 1, c, visit, heights[r][c])
dfs(r - 1, c, visit, heights[r][c])
dfs(r, c + 1, visit, heights[r][c])
dfs(r, c - 1, visit, heights[r][c])
여기서 2째줄(r-1), 4째줄(c-1)은 0보다 작으므로 조건문에 걸려 수행되지 않는다. 따라서 오른쪽, 아래쪽 으로만 탐색이 진행된다.
첫번째 줄을 수행해보자 dfs(r + 1, c, visit, heights[r][c]) r 이 1만큼 늘어나므로 아래 cell을 확인하게 된다. 각 값들을 매칭해본다면 dfs(1, 0, visit, 1) 이 될 것이다. 따라서 heights[1][0] 탐색하기 시작한다.
이런식으로 쭉 진행해본다면 pac 과 atl 이 다음과 같이 완성될 것이다.
# pac
{(0, 1), (1, 2), (0, 4), (2, 1), (4, 0), (0, 0), (3, 1), (1, 1), (0, 3), (2, 0), (1, 4), (3, 0), (0, 2), (2, 2), (1, 0), (1, 3)}
# atl
{(4, 4), (1, 3), (2, 4), (4, 0), (0, 4), (3, 4), (4, 3), (3, 1), (4, 2), (3, 0), (1, 4), (2, 3), (3, 3), (2, 2), (3, 2), (4, 1)}
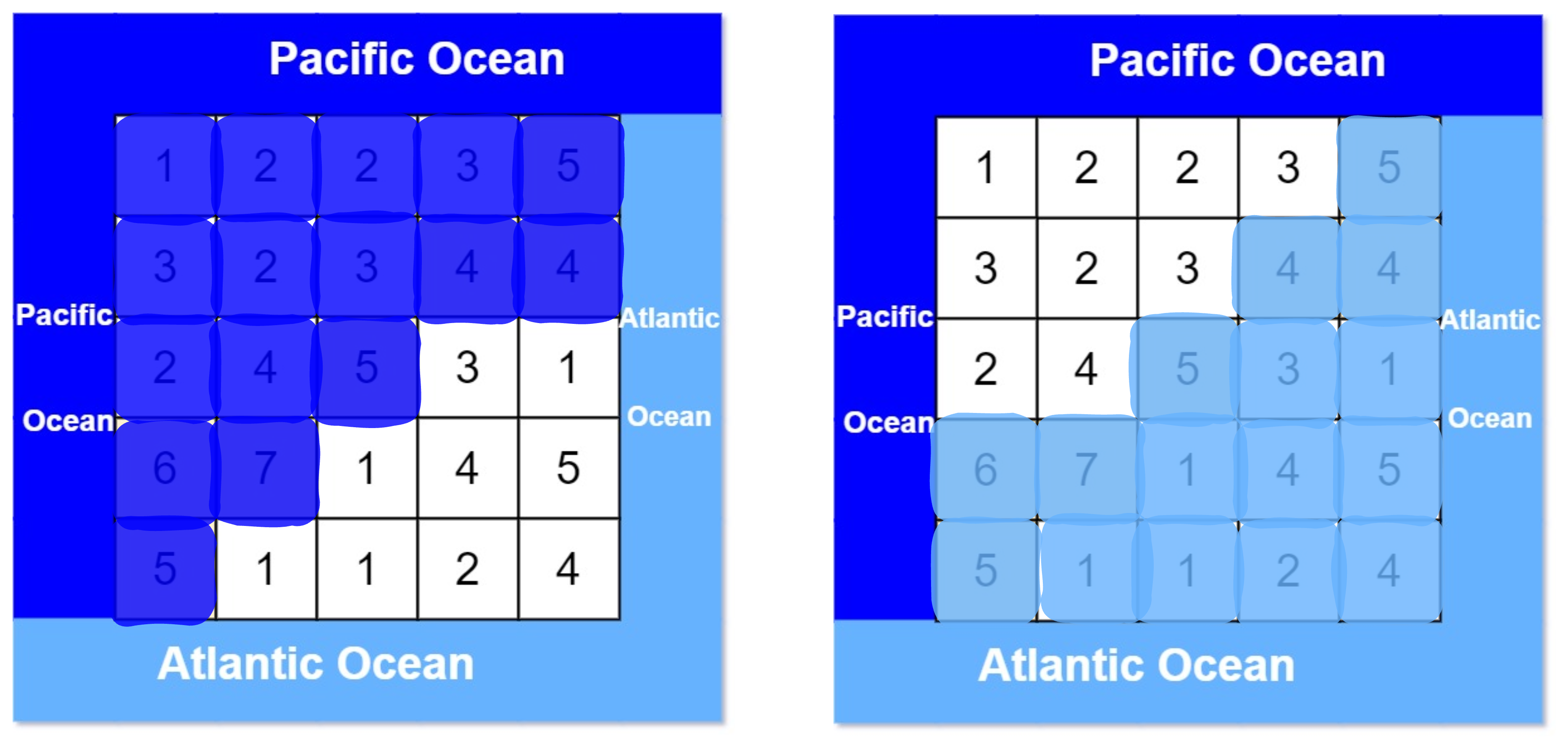
문제에서 요구하는 cell은 pac과 atl 에 모두 해당이 되어야 한다.
따라서 답은
[[0, 4], [1, 3], [1, 4], [2, 2], [3, 0], [3, 1], [4, 0]]
이 된다.
참고로 주어진 예시에서 (1,4) 같은 경우에는 직선적인 케이스만 고려해서는 찾을 수 없는 값이다. (1,4) 가 pacific에 들어가려면 (1,4) -> (1,3) -> (0,3) 순으로 거쳐야 한다. (왼쪽으로 갔다가 위로 올라간다) 따라서 dfs를 따라 모든 경로를 탐색해야 한다.
자바로 다시 풀기 (24.06.30)
public class Solution {
public List<List<Integer>> pacificAtlantic(int[][] heights) {
List<List<Integer>> result = new ArrayList<>();
for (int i = 0; i < heights.length; i++) {
for (int j = 0; j < heights[0].length; j++) {
System.out.printf("\n\ninit Flow : %d, %d\n", i, j);
Flow flow = new Flow();
dfs(flow, heights, Integer.MAX_VALUE, i, j);
if (flow.flowToAtlanticOcean && flow.flowToPacificOcean) {
result.add(List.of(i, j));
}
}
}
return result;
}
private void dfs(Flow flow, int[][] heights, int prev, int i, int j) {
if (i == -1 || j == -1) {
flow.flowToPacificOcean = true;
return;
}
if (i == heights.length || j == heights[0].length) {
flow.flowToAtlanticOcean = true;
return;
}
if (heights[i][j] == -1 || heights[i][j] > prev || flow.flowToAtlanticOcean && flow.flowToPacificOcean) {
return;
}
int currentHeight = heights[i][j];
heights[i][j] = -1;
dfs(flow, heights, currentHeight, i + 1, j);
dfs(flow, heights, currentHeight, i - 1, j);
dfs(flow, heights, currentHeight, i, j + 1);
dfs(flow, heights, currentHeight, i, j - 1);
heights[i][j] = currentHeight;
}
}
class Flow {
boolean flowToPacificOcean;
boolean flowToAtlanticOcean;
}
TC, SC
heights의 길이를 w, heights[0]의 길이를 h로 정의했을 때, 이 코드의 시간 복잡도는 O((w \* h)^2), 공간 복잡도는 O(w \* h) 이다. 시간 복잡도가 저렇게 나온 이유는 모든 좌표에 대해서 dfs를 진행하기 때문이다.