(Leetcode) 15 - 3Sum
New Year Gift - Curated List of Top 75 LeetCode Questions to Save Your Time
위 링크에 있는 추천 문제들을 시간이 있을때마다 풀어보려고 한다.
https://leetcode.com/problems/3sum/description/
medium 문제이다. 하지만 정답률이 매우 낮은 문제다.
단순히 for 문으로 3가지 조합을 찾을 경우에는 O(n^3) 으로 최대 3000^3 까지 가야하므로 이 방식은 피해야 할 것이라는 가정하에 진행하였다.
그러면 어떤 경우에 문제가 요구하는 조건 (3가지 수를 더했을 때 0이 되는 경우) 을 만족할 수 있을까 생각해보면 다음과 같았다.
- [0, 0, 0]
- 0 이 포함된 경우 [0, a, -a]
- a = -(b + c) 인 경우 [a, b, c]
그리고 이를 코드로 구현해보았다.
내가 작성한 풀이
class Solution {
public List<List<Integer>> threeSum(int[] nums) {
List<List<Integer>> result = new ArrayList<>();
Map<Integer, Integer> map = new HashMap<>();
for (int num : nums) {
map.put(num, map.getOrDefault(num, 0) + 1);
}
// case 1 : 0이 3개 있을 경우
int count = map.getOrDefault(0, 0);
if (count > 2) {
result.add(List.of(0, 0, 0));
}
// case 2 : 0이 있을 경우
if (count > 0) {
for (int num : map.keySet()) {
System.out.println("num : " + num);
// 중복을 방지하기 위해 0 이나 음수는 체크하지 않음
if (num > 0 && map.containsKey(num) && map.containsKey(-num)) {
result.add(List.of(-num, 0, num));
}
}
}
// case 3 : a = -(b + c) 인 경우 (a가 1일 경우는 불가능함. case1에 포함됨)
for (int num : map.keySet()) {
if (num > 1) {
for (int i = num - 1; i > num / 2 - (num % 2 == 0 ? 1 : 0); i--) {
int a = -i;
int b = -num + i; // -(num - i)
if (map.containsKey(a) && map.containsKey(b)) {
if (a < b) {
result.add(List.of(a, b, num));
} else if (a > b) {
result.add(List.of(b, a, num));
} else if (map.get(a) > 1) {
result.add(List.of(a, a, num));
}
}
}
} else if (num < -1) {
int abs = Math.abs(num);
for (int i = abs - 1; i > abs / 2 - (num % 2 == 0 ? 1 : 0); i--) {
int a = i;
int b = abs - i;
if (map.containsKey(a) && map.containsKey(b)) {
if (a < b) {
result.add(List.of(num, a, b));
} else if (a > b) {
result.add(List.of(num, b, a));
} else if (map.get(a) > 1) {
result.add(List.of(a, a, num));
}
}
}
}
}
return result;
}
}
통과는 하긴 하는데 아쉽게도 이 방법은 정말 아슬아슬하게 통과한다.
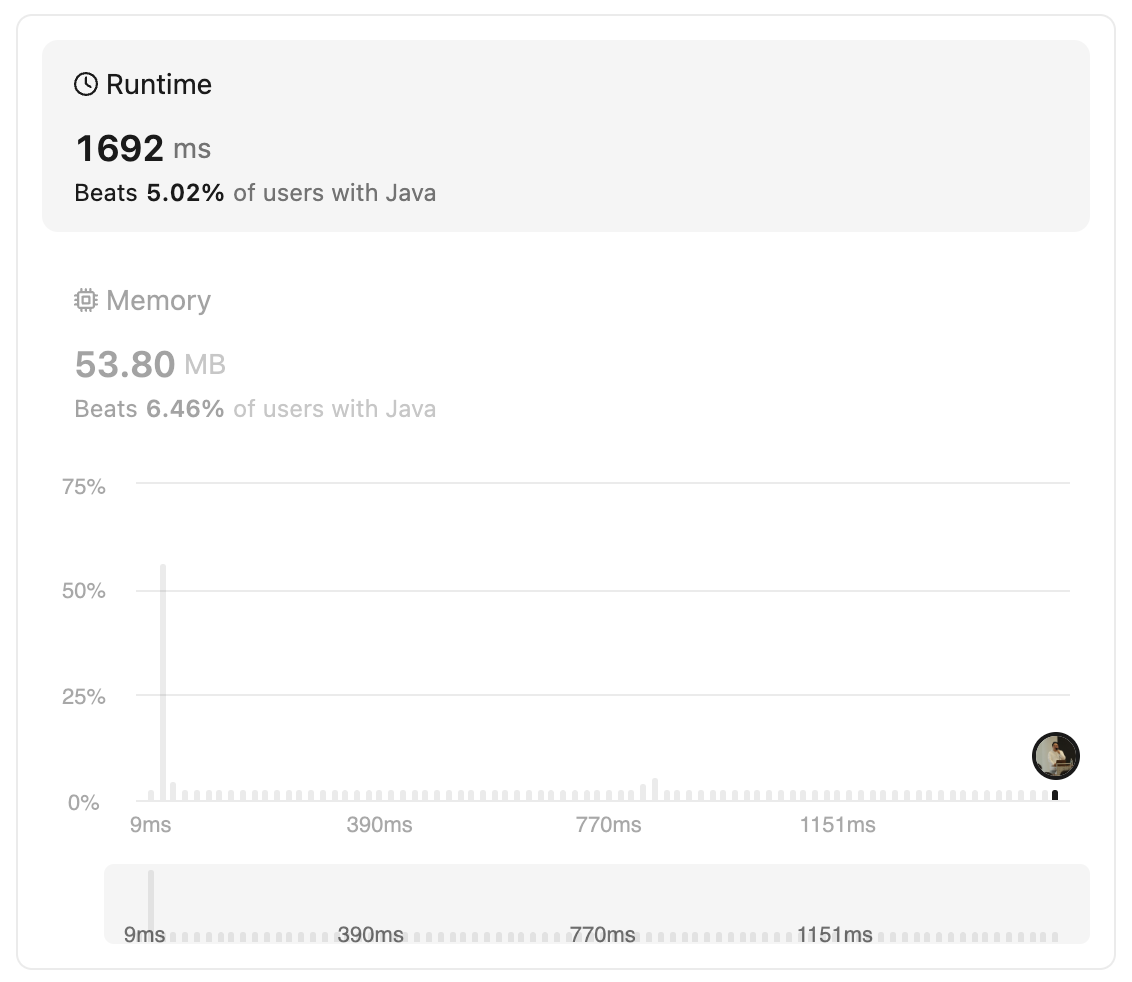
개선해보기
case3 의 속도가 문제다. case3 에 대해서 아래와 같이 개선해보았다.
// case 3 : a = -(b + c) 인 경우 (a가 1일 경우는 불가능함. case1에 포함됨)
Set<String> keySet = new HashSet<>();
for (int a : map.keySet()) {
for (int b : map.keySet()) {
if (a == 0 || b == 0) {
continue;
}
if(a == b) {
if(map.get(a) == 1) {
continue;
}
}
int twoSum = a + b;
if(twoSum == 0) {
continue;
}
if (a == -twoSum || b == -twoSum) {
if (map.get(-twoSum) == 1) {
continue;
}
}
if(map.containsKey(-twoSum)) {
List<Integer> list = new ArrayList<>(List.of(a,b, -twoSum));
Collections.sort(list);
String key = String.format("%d-%d-%d", list.get(0), list.get(1), list.get(2));
if(!keySet.contains(key)){
result.add(list);
keySet.add(key);
}
}
}
}
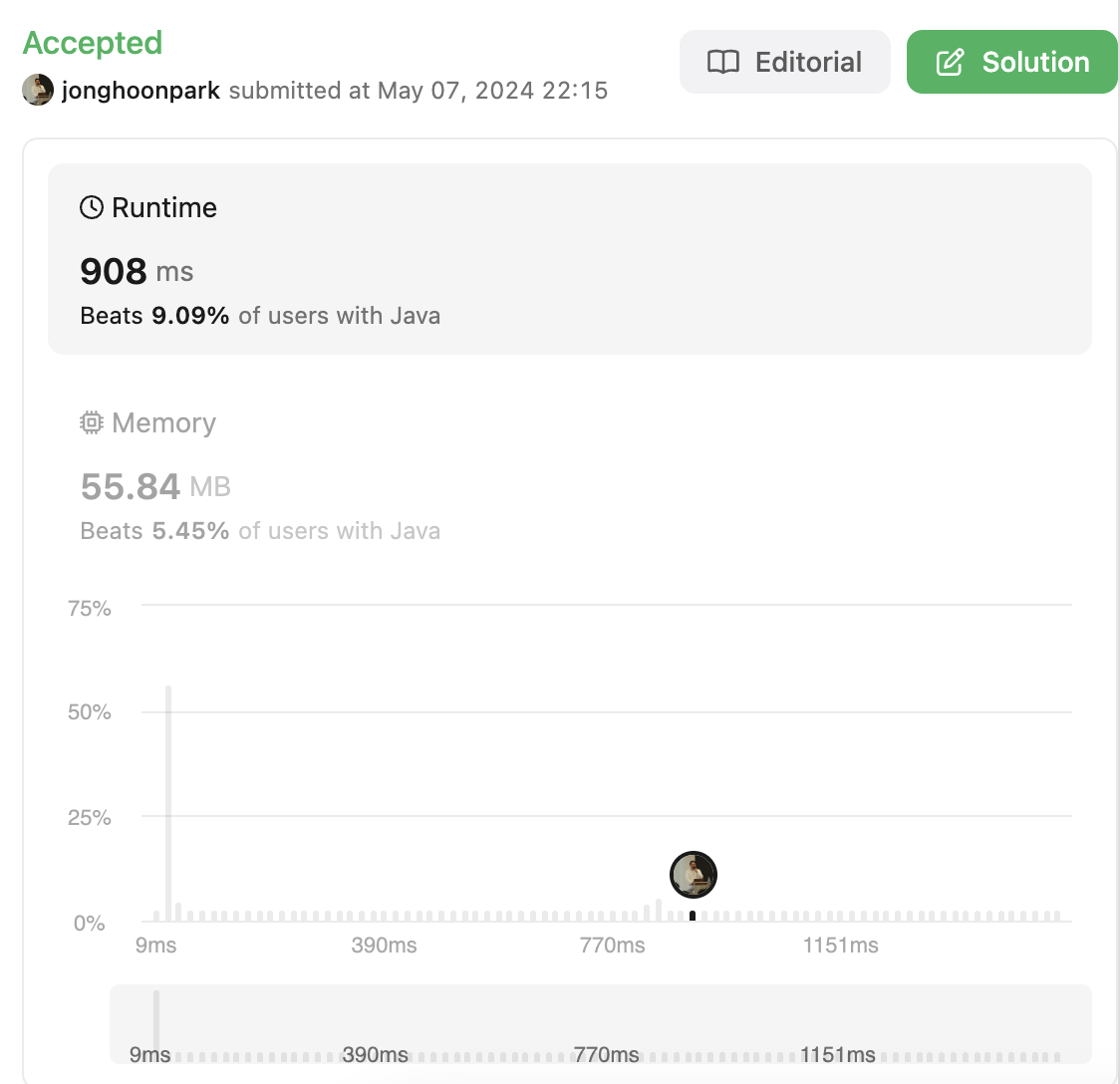
이전보다는 나아진 것을 볼 수 있다.
또 개선해보기
아무래도 String 으로 key를 만드는 부분이 거슬린다.
해당 부분을 제거하기 위해 두개의 set을 추가해보았다.
Set<Integer> checkDone = new HashSet<>();
List<Integer> keySetList = new ArrayList<>(map.keySet().stream().toList());
Collections.sort(keySetList);
for (int a : keySetList) {
int aCount = map.get(a);
Set<Integer> checkDone2 = new HashSet<>();
for (int b : keySetList) {
if (a == 0 || b == 0) {
continue;
}
int twoSum = -(a + b);
if (twoSum == 0) {
continue;
}
int twoSumCount = map.getOrDefault(twoSum, 0);
if (twoSumCount == 0) {
continue;
}
if (a == b && aCount == 1) {
continue;
}
if (a == twoSum || b == twoSum) {
if (twoSumCount == 1) {
continue;
}
}
if (checkDone.contains(b) || checkDone.contains(twoSum)) {
continue;
}
if (checkDone2.contains(b) || checkDone2.contains(twoSum)) {
continue;
}
if (b > twoSum) {
checkDone2.add(twoSum);
result.add(List.of(a, twoSum, b));
} else {
checkDone2.add(b);
result.add(List.of(a, b, twoSum));
}
}
checkDone.add(a);
}
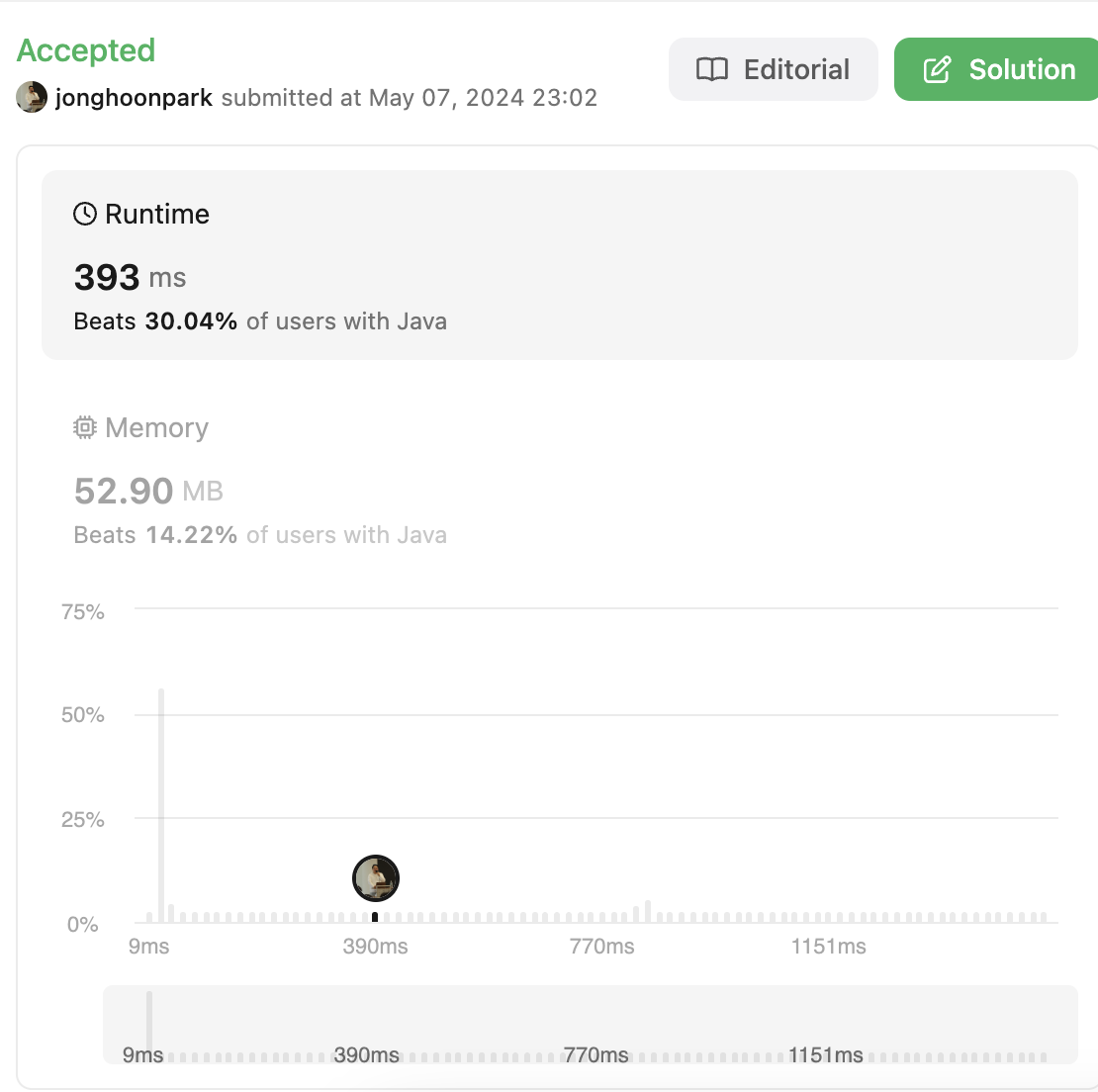
또 다시 이전보다는 나아진 것을 볼 수 있다.
TC, SC
최종적으로 시간 복잡도는 O(n^2), 공간 복잡도는 O(n^2) 이다.
모범 답안
class Solution {
public List<List<Integer>> threeSum(int[] nums) {
List<List<Integer>> result = new ArrayList<>();
Arrays.sort(nums);
for (int i = 0; i < nums.length - 2 && nums[i] <= 0; i++) {
if (i != 0 && nums[i] == nums[i - 1]) continue;
twoSum(-nums[i], nums, i + 1, result);
}
return result;
}
private void twoSum(int target, int[] nums, int startIndex, List<List<Integer>> result) {
int i = startIndex;
int j = nums.length - 1;
while (i < j) {
if (nums[i] + nums[j] < target) {
i++;
continue;
}
if (nums[i] + nums[j] > target) {
j--;
continue;
}
result.add(Arrays.asList(-target, nums[i], nums[j]));
i++;
j--;
while (j > i && nums[j] == nums[j + 1])
j--;
}
}
}
- treesum 을 twosum 으로 나누어 생각한다.
- nums 를 이미 정렬하였기 때문에
nums[i] == nums[i - 1]조건을 만족하면 스킵(continue)하여 중복 입력을 방지한다. i < nums.length - 2 && nums[i] <= 0
동작 과정
example input : [-4, -2, -2, -2, 0, 1, 2, 2, 2, 3, 3, 4, 4, 6, 6]
i = 0
- twoSum(-nums[0], nums, 1, result) -> twoSum(4, nums, 1, result)
- i = startIndex = 1, j = nums.length - 1
- i < j (중간에서 만나기 때문에 반목문을 다 돌지 않아도 된다.)
- nums[i] + nums[j] < target : i 값이 커져야 target에 가까워짐 (i++)
- nums[i] + nums[j] > target : j 값이 커져야 target에 가까워짐 (j–)
- nums[i] + nums[j] == target : result에 등록
- 등록 후에는 i++, j– 진행 하여 다른 값이 없는지 추가로 확인 (이 때 j가 중복된 값이 나오지 않도록 while로 반복)
- 여기서 j 가 아닌 i 를 옮겨도 무방하다.
- 등록 후에는 i++, j– 진행 하여 다른 값이 없는지 추가로 확인 (이 때 j가 중복된 값이 나오지 않도록 while로 반복)
- twoSum(-nums[0], nums, 1, result) -> twoSum(4, nums, 1, result)
…
j가 아니라 i를 옮기는 코드
while (j > i && nums[i] == nums[i - 1])
i++;
TC, SC
모범답안도 동일하게 시간 복잡도는 O(n^2)이다. 시간 복잡도는 이전과 동일하지만 실제 동작은 20-30ms 로 끝나기 떄문에 약 33배 차이가 난다. 공간 복잡도에서는 큰 의미가 있는데 결과값을 고려하지 않은 알고리즘 자체의 공간 복잡도는 O(1) 이다.
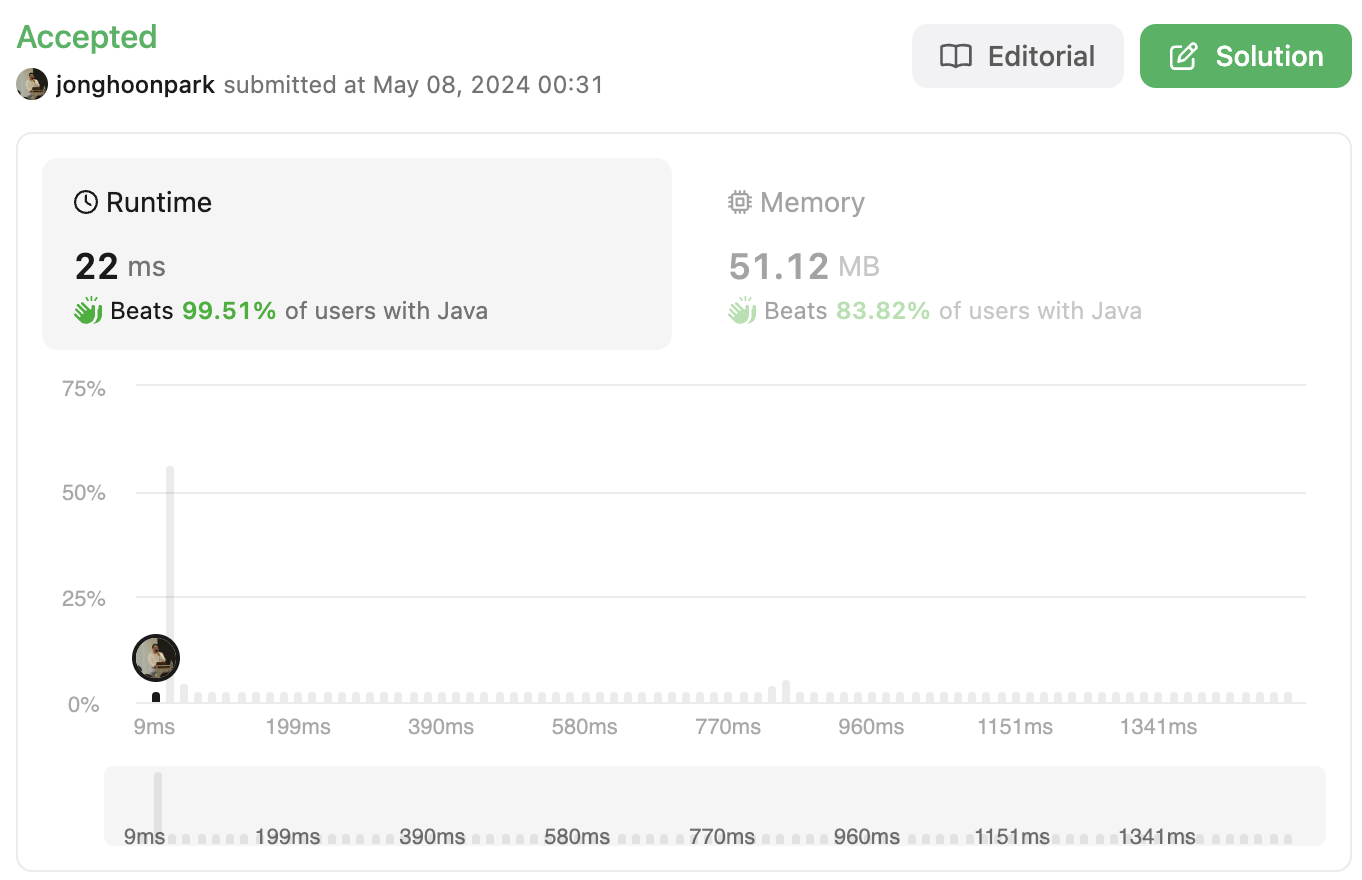
다시 풀어보기 (240529)
지난번에 풀었던 기억을 되살려서 이번에는 도움 없이 다시 풀어봤다. 코드를 좀 더 이해하기 쉽게 배치했다고 생각한다.
public List<List<Integer>> threeSum(int[] nums) {
Arrays.sort(nums);
List<List<Integer>> result = new ArrayList<>();
int lastOne = Integer.MIN_VALUE;
for (int i = 0; i < nums.length - 1; i++) {
int num = nums[i];
if (lastOne == num) {
continue;
}
twoSum(result, nums, i);
lastOne = num;
}
return result;
}
public void twoSum(List<List<Integer>> result, int[] nums, int targetIndex) {
int target = -nums[targetIndex];
int i = targetIndex + 1;
int j = nums.length - 1;
while (i < j) {
int twoSum = nums[i] + nums[j];
if (target > twoSum) {
i++;
}
if (target < twoSum) {
j--;
}
if (target == twoSum) {
result.add(List.of(-target, nums[i], nums[j]));
int current = nums[i];
while (i < nums.length - 2 && current == nums[i + 1]) {
i++;
}
i++;
}
}
}